Recursion means “defining a problem in terms of itself”. This can be a very powerful tool in writing algorithms. Recursion comes directly from Mathematics, where there are many examples of expressions written in terms of themselves. For example, the Fibonacci sequence is defined as: F(i) = F(i-1) + F(i-2)
The recursive function has two parts:
- Base Case
- Recursive Structure
Base Case: The smallest version of the problem for which we already know the solution or a terminating condition where a function can return the result immediately.
Recursive Structure: Finding the solution to a problem via the solution of its smaller sub-problems. Here function must call itself to break the current problem down to a simpler level.
The typical recursive coding takes the following form:
if (test for simple case) {
return (simple computation without recursion);
} else {
return (recursive solution);
}
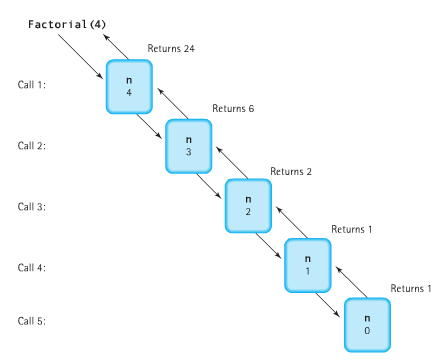
The below image depicts how Recursion works:

Program 1
#include <iostream>
using namespace std;
void countDown(int count)
{
cout << "push " << count << '\n';
countDown(count-1); // countDown() calls itself recursively
}
int main()
{
countDown(5);
return 0;
}
Program 2
#include <iostream>
using namespace std;
void countDown(int count)
{
cout << "push " << count << '\n';
if (count > 1) // termination condition
countDown(count-1);
cout << "pop " << count << '\n';
}
int main()
{
countDown(5);
return 0;
}
Program 3
#include <iostream>
using namespace std;
int sumTo(int);
int main()
{
cout << sumTo(5);
return 0;
}
// return the sum of all the numbers between 1 and value (inclusive)
int sumTo(int value)
{
if (value <= 0)
return 0; // base case (termination condition)
else if (value == 1)
return 1; // base case (termination condition)
else
return sumTo(value - 1) + value; // recursive function call
}
Program 4
#include<iostream>
using namespace std;
void print_backwards();
int main()
{
print_backwards();
cout << "\n";
return 0;
}
void print_backwards()
{
char character;
cout << "Enter a character ('.' to end program): ";
cin >> character;
if (character != '.')
{
print_backwards();
cout << character;
}
}
Program 5
#include<iostream>
using namespace std;
int sum(int );
int main()
{
int number, result;
cout << "Enter a positive integer: ";
cin >> number;
result = sum(number);
cout << "sum - " << result;
return 0;
}
int sum(int num)
{
if (num!=0)
return num + sum(num-1); // sum() function calls itself
else
return num;
}
Program 6
#include <iostream>
using namespace std;
int factorial(int n)
{
if(n!=0)
return n*factorial(n-1);
return 1;
}
int main()
{
int num,facto;
cout << "Enter a number: ";
cin >> num;
facto=factorial(num);
cout << facto;
return 0;
}
Program 7
#include <iostream>
using namespace std;
double power(double,int);
int main()
{
double base,pow;
int exponent;
cout << "Enter Base: ";
cin >> base;
cout << "Enter Exponent: ";
cin >> exponent;
pow=power(base,exponent);
cout << "The value of " << base
<< " to the power of " << exponent
<< " is " << pow;
return(0);
}
double power (double Num,int Exp)
{
if(Exp <=0 ) // Exp is non-positive
return(1);
else
return(Num * power(Num, Exp-1));
}
Program 8
#include <iostream>
using namespace std;
void normalPrint(char *s)
{
if(*s) {
putchar(*s);
normalPrint(s+1);
}
}
void reversePrint(char *s)
{
if(*s) {
reversePrint(s+1);
putchar(*s);
}
}
int main()
{
char *str = "Hadji Tejuco";
normalPrint(str);
cout << endl;
reversePrint(str);
cout << endl;
return 0;
}
Program 9
#include <iostream>
using namespace std;
int n_to_the_kth_power(int n, int k)
{
if (k == 0)
return 1;
else
return n * n_to_the_kth_power(n, k-1);
}
int main ()
{
int n = 2, k = 10;
while (k >= 0) {
cout << n << "**" << k << " = " << n_to_the_kth_power(n,k) << endl;
k--;
}
while(1) {}
return 0;
}
Output
2**10 = 1024 2**9 = 512 2**8 = 256 2**7 = 128 2**6 = 64 2**5 = 32 2**4 = 16 2**3 = 8 2**2 = 4 2**1 = 2 2**0 = 1
Program 10
#include <iostream>
using namespace std;
int gcd (int m, int n)
{
if(n == 0) return m;
cout << "gcd(" << m << ',' << n <<')'<< endl;
return gcd(n, m % n);
}
int main()
{
cout << "gcd = " << gcd(1256636, 1630968) << endl;
return 0;
}
Output
gcd = gcd(1256636,1630968) gcd(1630968,1256636) gcd(1256636,374332) gcd(374332,133640) gcd(133640,107052) gcd(107052,26588) gcd(26588,700) gcd(700,688) gcd(688,12) gcd(12,4) 4
Program 11
#include <iostream>
using namespace std;
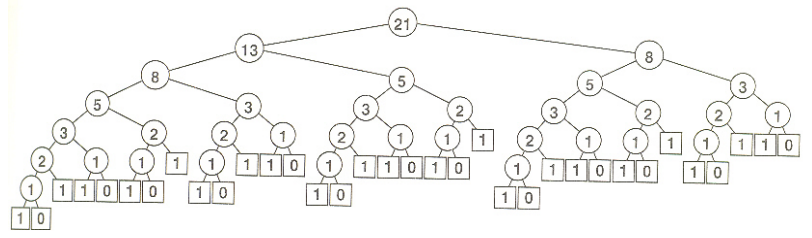
int fibo(int n)
{
if(n == 0 || n == 1) return n;
return fibo(n-1)+fibo(n-2);
}
int fibo_iter(int n)
{
if(n == 0 || n == 1) return n;
int f0 = 0, f1 = 1, f2;
for(int i = 2; i <= n; i++) {
f2 = f0 + f1;
f0 = f1;
f1 = f2;
}
return f2;
}
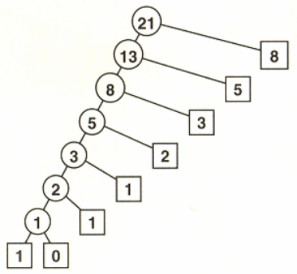
int fibo_dynamic(int n)
{
static int saved[100] = {0};
if(saved[n] != 0) return saved[n];
if(n == 0 || n == 1) {
saved[n] = n;
return saved[n];
}
saved[n] = fibo_dynamic(n-1)+fibo_dynamic(n-2);
return saved[n];
}
int main()
{
int i;
int n = 15;
cout << "recursive Fibonacci " << endl;
for(i = 0; i < n; i++)
cout << fibo(i) << " ";
cout << endl;
cout << "iterative Fibonacci " << endl;
for(i = 0; i < n; i++)
cout << fibo_iter(i) << " ";
cout << endl;
cout << "dynamic Fibonacci " << endl;
for(i = 0; i < n; i++)
cout << fibo_dynamic(i) << " ";
cout << endl;
return 0;
}
Output
recursive Fibonacci 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 iterative Fibonacci 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 dynamic Fibonacci 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
Program 11 (Palindrome)
#include <iostream>
using namespace std;
int reverse_digits(int n, int temp)
{
if (n == 0)
return temp;
temp = (temp * 10) + (n % 10);
return reverse_digits(n / 10, temp);
}
int main()
{
int num;
cout<<"Enter the number to check palindrome:"; cin>>num;
int result = reverse_digits(num, 0);
if (result == num)
cout << "Number "<<num<<" is a palindrome" << endl;
else
cout << "Number "<<num<<" is not a palindrome"<< endl;
return 0;
}