Bubble Sort
Bubble Sort is the simplest of the sorting techniques.
In the bubble sort technique, each of the elements in the list is compared to its adjacent element. Thus if there are n elements in list A, then A[0] is compared to A[1], A[1] is compared to A[2] and so on.
After comparing if the first element is greater than the second, the two elements are swapped then.
Bubble Sort Technique
Using the bubble sort technique, sorting is done in passes or iteration. Thus at the end of each iteration, the heaviest element is placed at its proper place in the list. In other words, the largest element in the list bubbles up.
We have given a general algorithm of bubble sort technique below.
General Algorithm
Step 1: For i = 0 to N-1 repeat Step 2
Step 2: For J = i + 1 to N – I repeat
Step 3: if A[J] > A[i]
Swap A[J] and A[i]
[End of Inner for loop]
[End if Outer for loop]
Step 4: Exit
Here is a pseudo-code for bubble sort algorithm, where we traverse the list using two iterative loops.
In the first loop, we start from the 0th element and in the next loop, we start from an adjacent element. In the inner loop body, we compare each of the adjacent elements and swap them if they are not in order. At the end of each iteration of the outer loop, the heaviest element bubbles up at the end.
Pseudocode
Procedure bubble_sort (array , N)
array – list of items to be sorted
N – size of array
begin
swapped = false
repeat
for I = 1 to N-1
if array[i-1] > array[i] then
swap array[i-1] and array[i]
swapped = true
end if
end for
until not swapped
end procedure
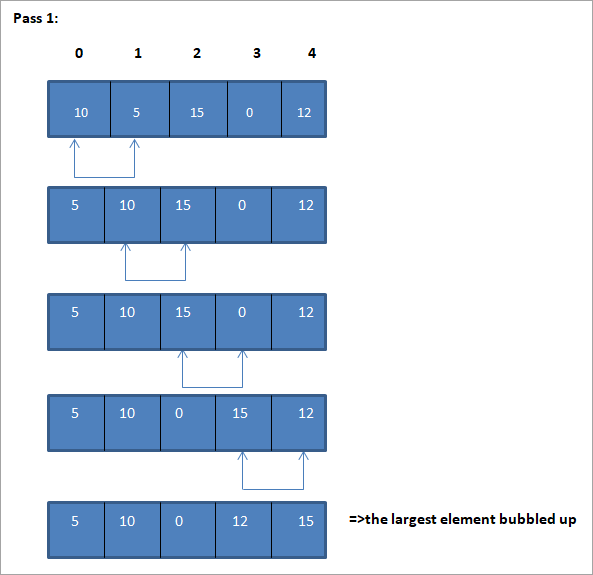
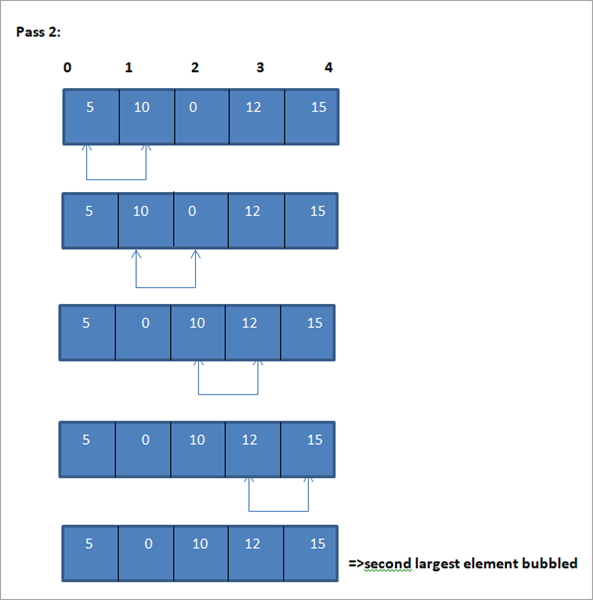
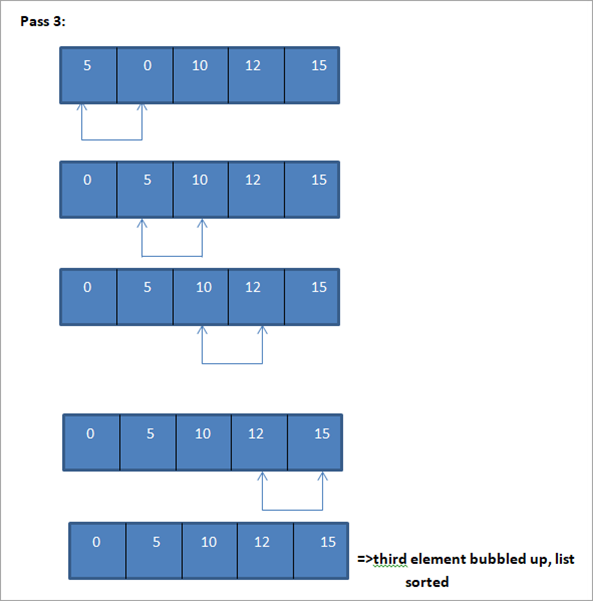
Array entirely sorted.
The above illustration can be summarized in a tabular form as shown below:
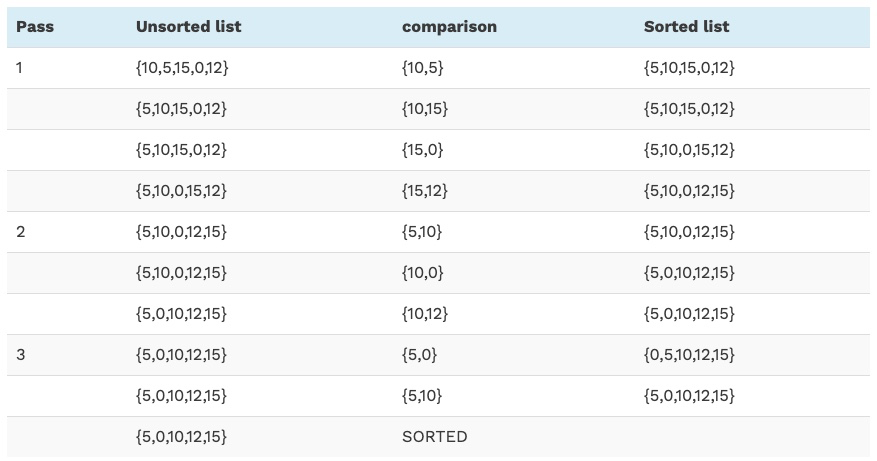
As shown in the illustration, with every pass, the largest element bubbles up to the last thereby sorting the list with every pass. As mentioned in the introduction, each element is compared to its adjacent element and swapped with one another if they are not in order.
Thus as shown in the illustration above, at the end of the first pass, if the array is to be sorted in ascending order, the largest element is placed at the end of the list. For the second pass, the second largest element is placed at the second last position in the list and so on.
When we reach N-1 (where N is a total number of elements in the list) passes, we will have the entire list sorted.
SELECTION SORT
The selection sort technique first selects the smallest element in the array and swaps it with the first element in the array.
Next, it swaps the second smallest element in the array with the second element and so on. Thus for every pass, the smallest element in the array is selected and put in its proper position until the entire array is sorted.
Selection sort is quite a straightforward sorting technique as the technique only involves finding the smallest element in every pass and placing it in the correct position.
Selection sort works efficiently when the list to be sorted is of small size but its performance is affected badly as the list to be sorted grows in size.
Hence we can say that selection sort is not advisable for larger lists of data.
General Algorithm
The General Algorithm for selection sort is given below:
Selection Sort (A, N)
Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
Step 2: Call routine smallest(A, K, N,POS)
Step 3: Swap A[K] with A [POS]
[End of loop]
Step 4: EXIT
Routine smallest (A, K, N, POS)
- Step 1: [initialize] set smallestElem = A[K]
- Step 2: [initialize] set POS = K
- Step 3: for J = K+1 to N -1,repeat
if smallestElem > A [J]
set smallestElem = A [J]
set POS = J
[if end]
[End of loop] - Step 4: return POS
Pseudocode For Selection Sort
Procedure selection_sort(array,N)
array – array of items to be sorted
N – size of array
begin
for I = 1 to N-1
begin
set min = i
for j = i+1 to N
begin
if array[j] < array[min] then
min = j;
end if
end for
//swap the minimum element with current element
if minIndex != I then
swap array[min[] and array[i]
end if
end for
end procedure
An example to illustrate this selection sort algorithm is shown below.
Illustration
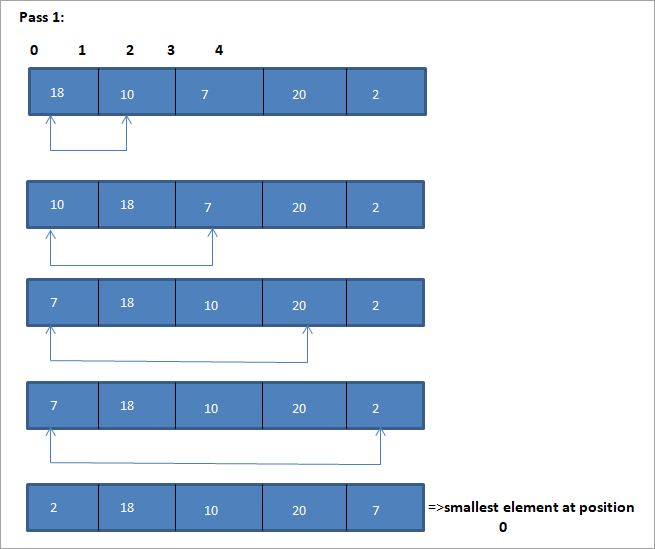
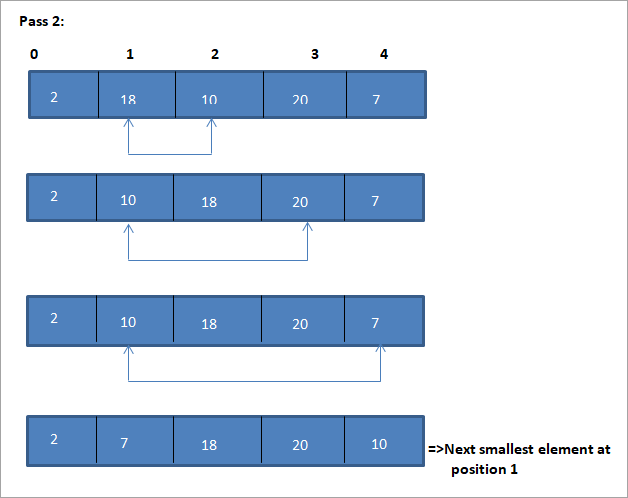
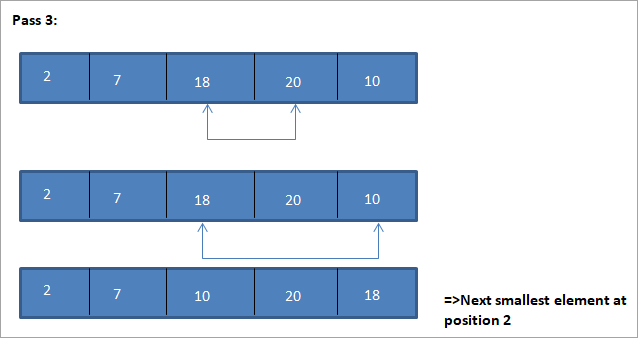
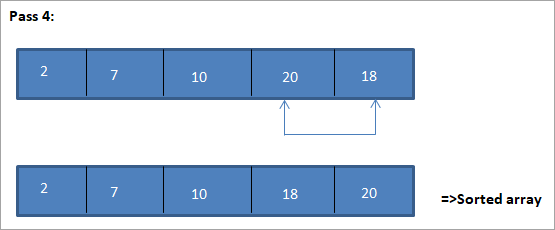

From the illustration, we see that with every pass the next smallest element is put in its correct position in the sorted array. From the above illustration, we see that in order to sort an array of 5 elements, four passes were required. This means in general, to sort an array of N elements, we need N-1 passes in total.
Insertion Sort
Insertion sort is a sorting technique which can be viewed in a way which we play cards at hand. The way we insert any card in a deck or remove it, insertion sorts works in a similar way.
Insertion sort algorithm technique is more efficient than the Bubble sort and Selection sort techniques but is less efficient than the other techniques like Quicksort and Merge sort.
In the insertion sort technique, we start from the second element and compare it with the first element and put it in a proper place. Then we perform this process for the subsequent elements.
We compare each element with all its previous elements and put or insert the element in its proper position. Insertion sort technique is more feasible for arrays with a smaller number of elements. It is also useful for sorting linked lists.
Linked lists have a pointer to the next element (in case of a singly linked list) and a pointer to the previous element as well (in case of a doubly linked list). Hence it becomes easier to implement insertion sort for a linked list.
Let us explore all about Insertion sort in this tutorial.
General Algorithm
Step 1: Repeat Steps 2 to 5 for K = 1 to N-1
Step 2: set temp = A[K]
Step 3: set J = K – 1
Step 4: Repeat while temp <=A[J]
set A[J + 1] = A[J]
set J = J – 1
[end of inner loop]
Step 5: set A[J + 1] = temp
[end of loop]
Step 6: exit
Thus, in the insertion sort technique, we start from the second element as we assume that the first element is always sorted. Then from the second element to the last element, we compare each element to all of its previous elements and the put that element in the proper position.
Pseudocode
The pseudo code for insertion sort is given below.
procedure insertionSort(array,N )
array – array to be sorted
N- number of elements
begin
int freePosition
int insert_val
for i = 1 to N -1 do:
insert_val = array[i]
freePosition = i
//locate free position to insert the element
whilefreePosition> 0 and array[freePosition -1] >insert_val do:
array [freePosition] = array [freePosition -1]
freePosition = freePosition -1
end while
//insert the number at free position
array [freePosition] = insert_val
end for
end procedure
Given above is the pseudo code for Insertion sort, next, we will illustrate this technique in the following example.
Illustration
The array to be sorted is as follows:
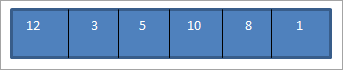
Now for each pass, we compare the current element to all its previous elements. So in the first pass, we start with the second element.
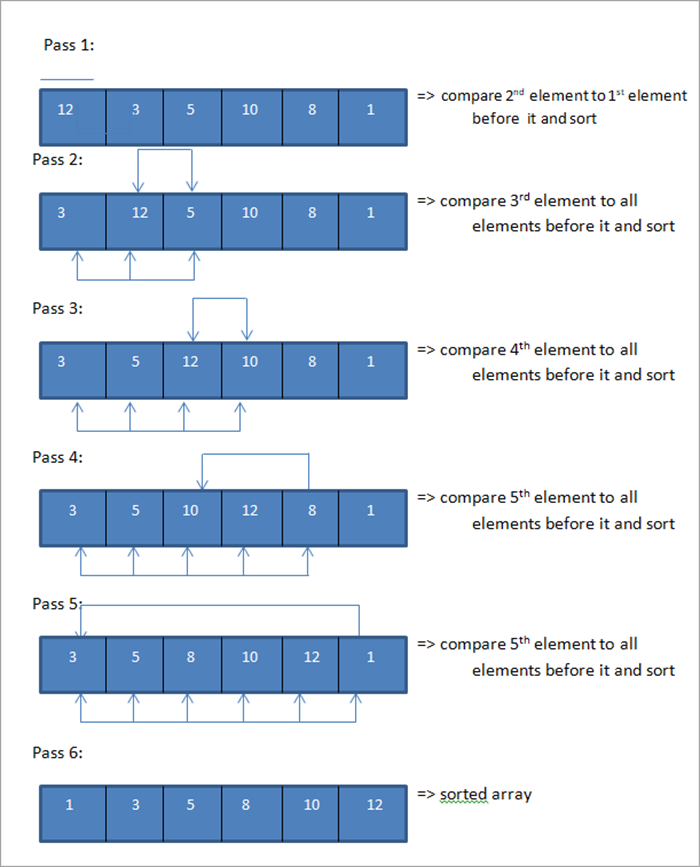
Thus we require N number of passes to completely sort an array containing N number of elements.
The above illustration can be summarized in a tabular form:
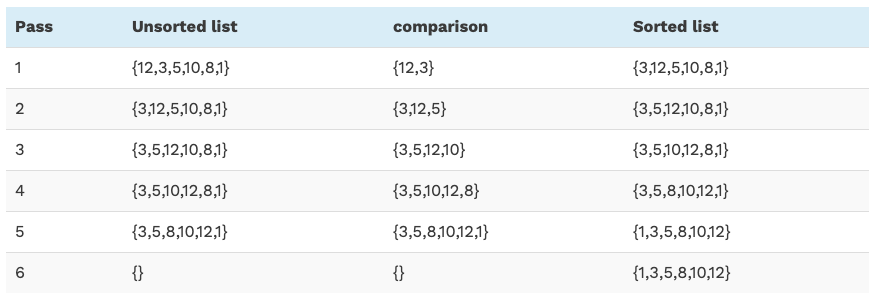
As shown in the above illustration, we begin with the 2nd element as we assume that the first element is always sorted. So we begin with comparing the second element with the first one and swap the position if the second element is less than the first.
This comparison and swapping process positions two elements in their proper places. Next, we compare the third element to its previous (first and second) elements and perform the same procedure to place the third element in the proper place.
In this manner, for each pass, we place one element in its place. For the first pass, we place the second element in its place. Thus in general, to place N elements in their proper place, we need N-1 passes.
Shell Sort
Shell sort is often termed as an improvement over insertion sort. In insertion sort, we take increments by 1 to compare elements and put them in their proper position.
In shell sort, the list is sorted by breaking it down into a number of smaller sublists. It’s not necessary that the lists need to be with contiguous elements. Instead, shell sort technique uses increment i, which is also called “gap” and uses it to create a list of elements that are “i” elements apart.
The general algorithm for shell sort is given below.
shell_sort (A, N)
where A – list to be sorted; N – gap_size
set gap_size = N, flag = 1
while gap_size > 1 or flag = 1, repeat
begin
set flag = 0
set gap_size = (gap_size + 1)/2
end
for i = 0 to i< (N-gap_size) repeat
begin
if A[i + gap_size] > A[i]
swap A[i + gap_size], A[i]
set flag = 0
end
end
Thus in the above algorithm, we first set N which is the gap for sorting the array A using shell sort. In the next step, we divide the array into sub-arrays by using the gap. Then in the next step, we sort each of the sub-arrays so that at the end of the loop we will get a sorted array.
Next, let us consider a detailed example to better understand the shell sort using a pictorial representation.
Illustration
Let us illustrate the Shell sort with an Example.
Consider the following array of 10 elements.

If we provide a gap of 3, then we will have the following sub-lists with each element that is 3 elements apart. We then sort these three sublists.
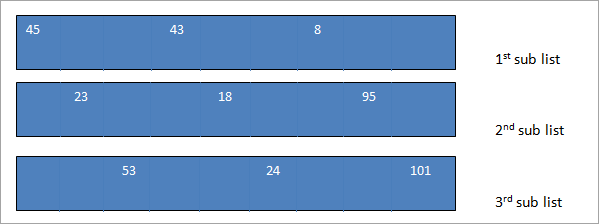
The sorted sub-lists and the resultant list that we obtain after combining the three sorted sublists are shown below.
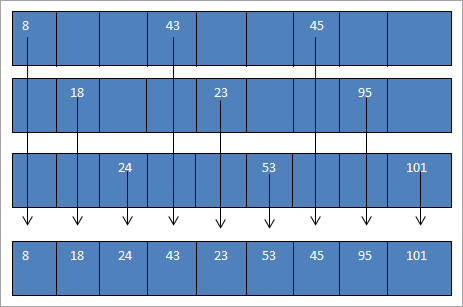
The above array that we have obtained after merging the sorted subarrays is nearly sorted. Now we can perform insertion sort on this list and sort the entire array. This final step is shown below for your reference.
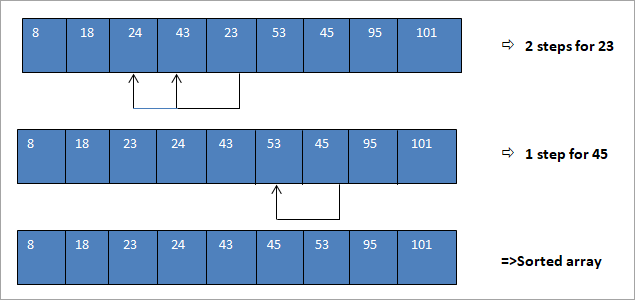
As seen above, after performing shell sort and merging the sorted sublists, we only required three moves to completely sort the list. Thus we can see that we can significantly reduce the number of steps required to sort the array.
SHELL SORT
Shell sort is often termed as an improvement over insertion sort. In insertion sort, we take increments by 1 to compare elements and put them in their proper position.
In shell sort, the list is sorted by breaking it down into a number of smaller sublists. It’s not necessary that the lists need to be with contiguous elements. Instead, shell sort technique uses increment i, which is also called “gap” and uses it to create a list of elements that are “i” elements apart.
The general algorithm for shell sort is given below.
shell_sort (A, N)
where A – list to be sorted; N – gap_size
set gap_size = N, flag = 1
while gap_size > 1 or flag = 1, repeat
begin
set flag = 0
set gap_size = (gap_size + 1)/2
end
for i = 0 to i< (N-gap_size) repeat
begin
if A[i + gap_size] > A[i]
swap A[i + gap_size], A[i]
set flag = 0
end
End
Thus in the above algorithm, we first set N which is the gap for sorting the array A using shell sort. In the next step, we divide the array into sub-arrays by using the gap. Then in the next step, we sort each of the sub-arrays so that at the end of the loop we will get a sorted array.
Next, let us consider a detailed example to better understand the shell sort using a pictorial representation.
Illustration
Let us illustrate the Shell sort with an Example.
Consider the following array of 10 elements.

If we provide a gap of 3, then we will have the following sub-lists with each element that is 3 elements apart. We then sort these three sublists.
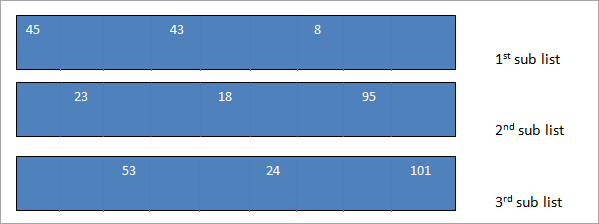
The sorted sub-lists and the resultant list that we obtain after combining the three sorted sublists are shown below.
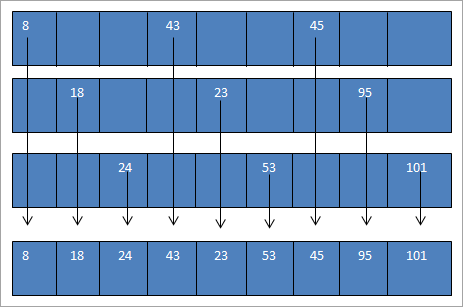
The above array that we have obtained after merging the sorted subarrays is nearly sorted. Now we can perform insertion sort on this list and sort the entire array. This final step is shown below for your reference.
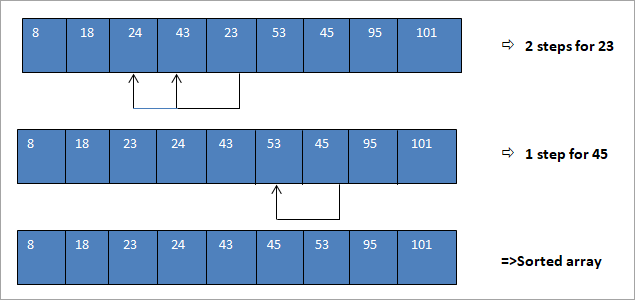
As seen above, after performing shell sort and merging the sorted sublists, we only required three moves to completely sort the list. Thus we can see that we can significantly reduce the number of steps required to sort the array.
The choice of increment to create sub-lists is a unique feature of shell sort.